go through: Dr. Yumeng Chen
“The world is not perfect. Every measurement should have error bars. This is what I learned as a student many years ago before entering a fluid dynamics lab. Now when I work in data assimilation (DA), this The sentence still echoes. Since neither observations nor model predictions are perfect, DA combines observations and predictions to provide an estimate of the most likely state of the modeled system, based on its error/uncertainty. An error bar that should reduce uncertainty compared to model predictions and observations.
As an important part of the climate system, Arctic sea ice regulates solar radiation, provides habitat for marine life, and affects human activities. As in various fields such as numerical weather prediction, marine ecosystems, and land surface modeling, the Arctic sea ice community operationally employs DA techniques to provide estimates of Arctic sea ice status for better predictions. Improved seasonal forecasts of Arctic sea ice through better initialization of sea ice concentration (percentage of Arctic sea ice in each grid cell) and sea ice thickness (Kimmritz et al., 2019). However, initial conditions are not the only source of uncertainty in Arctic sea ice. Numerical models can also be affected by incorrect parameters. These errors can bias Arctic sea ice predictions, especially in long-term simulations.
Fortunately, DA can also provide estimates of unobserved model fields and model parameters. How does DA estimate something we don't observe? This is based on the relationship between parameter errors and observational model predictions. This means that if we know the errors in model predictions from observations, using this relationship, we can infer and reduce the errors in the model parameters. In most operational DA methods, the relationship between parameters and prediction errors is represented by the error covariance derived from the numerical model. Therefore, the performance of parameter estimation using DA strongly depends on the dynamics of the numerical model.
This reliance on model dynamics can lead to problems with parameter estimation. For example, DA may provide incorrect estimates when multiple sets of model parameters lead to the same model prediction – which, if you know, indicates an ill-posed problem. Furthermore, parameter estimation may fail when the parameters are less sensitive to observed model fields compared to other sources of uncertainty. To demonstrate the potential problems with parameter estimation when prediction errors in observed model fields do not arise primarily from parameter errors, we can apply DA to estimate parameters in a new “purely dynamic” sea ice model developed in the scale-aware sea ice project (Chen et al., 2023).
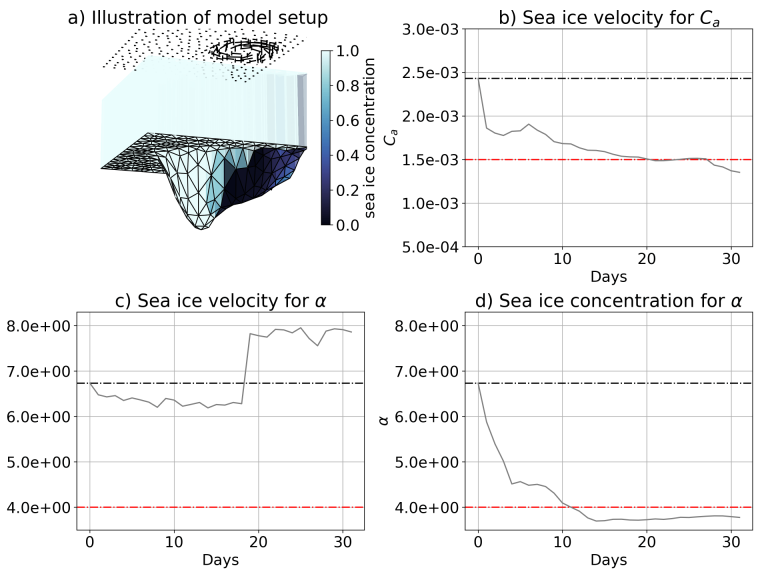
We set up an idealized experiment in which a patch of sea ice is subjected to periodic random storms (Fig. 1a). In this idealized setup, thermodynamics does not exist and wind is the only external forcing. In this purely dynamic sea ice model, depending on the state of the sea ice, the sea ice can elastically deform like a spring, permanently deform like a viscous fluid, and suddenly break under the action of its internal dynamics or external forces, resulting in the collapse of the sea ice. Damage and breakage. The initial state of the sea ice was not damaged, and the main error in the experimental setup came from random storm winds.

Figure 1: a) Schematic of the experimental setup, with the quiver showing the wind field, the sea ice in the middle of the area is thicker than at the boundary, and the sea ice concentration is constantly decreasing due to constant wind force; b) Estimation of air drag coefficient using sea ice velocity observations, c) Estimating damage parameters using observations of sea ice velocity, and d) estimating time series of damage parameters using observations of sea ice concentration.
In such an idealized setting, we can determine the true model states and parameters and assign errors to the parameters of our choice. An important model parameter of sea ice models is the air drag coefficient. This coefficient determines how wind affects sea ice speed. Errors in the wind field can be amplified or reduced by this coefficient of sea ice velocity.
Let us assume that the air drag coefficient is wrong and all other model parameters are correct. In this case, we can use DA to obtain very accurate estimates of the air drag coefficient when we use sea ice velocity observations (Fig. 1b). Another important model parameter for sea ice models is called the damage parameter. This parameter determines the response of sea ice movement to forces exerted on it when the sea ice is damaged. With lower damage parameter values, sea ice can behave like an elastic spring; with higher damage parameter values, sea ice can react more slowly to forces like a viscous fluid. However, sea ice velocity observations cannot provide reliable estimates of damage parameters when they are the only model parameters in error (Fig. 1c). Damage parameters cannot be reliably inferred from sea ice velocity because it is mainly affected by the wind field. In contrast, we see that incorporating sea ice concentration improves parameter estimates (Fig. 1d).
Here, our example shows that parameter estimation using DA can be challenging and must be performed with caution. However, DA remains a powerful tool for improving errors in models based on available observations.
References and further reading
Kimmritz, M., Counillon, F., Smedsrud, LH, Bethke, I., Keenlyside, N., Okawa, F., & Wang, Y. (2019). Effects of ocean and sea ice initialization on Arctic seasonal forecast skill. Journal of Advances in Earth System Modeling, 11, 4147–4166. https://doi.org/10.1029/2019MS001825
Chen, Y., Smith, P., Carrassi, A., Pasmans, I., Bertino, L., Bocquet, M., Finn, TS, Rampal, P., and Dansereau, V.: Multivariate state and parameter estimation using Maxwellian-elastic-brittle rheology data assimilation for sea ice models, EGUsphere [preprint], https://doi.org/10.5194/egusphere-2023-18092023.