go through: professor. David Ferreira
Recently, a colleague pointed out that in the subtropics of the Northern Hemisphere, the wind direction is around 30-40N (jet stream) and the westerly wind is 20-10N (trade wind). These winds make the ocean rotate clockwise. This is similar to thinking of the ocean as a solid plate rotating on an axis: if someone pushes the plate in one direction on one side and the opposite direction on the other side, the plate will rotate.

Figure 1: Observed mean ocean topography estimated from a combination of satellite measurements and ocean drifters from Maximenko et al. (2009). Data, charts and more details can be found here: https://apdrc.soest.hawaii.edu/projects/DOT/. The pink arrow represents the dominant wind, while the blue arrow shows the average current direction throughout the ocean depth.
Figure 1 shows dynamic ocean topography (DOT). Current tends to flow along the contours of the DOT. Focusing on the North Pacific, this figure highlights the most striking example of a subtropical gyre, with clockwise motion between approximately 10 and 40N (but these gyres occur in all basins). Applying solid plate reasoning to the Southern Hemisphere indicates that the circulations rotate counterclockwise (and they do! See Figure 1).
“Correlation” analysis supports the explanation of the physical sector. All subtropical gyres rotate in the direction of the wind, and actually to some extent this is a good explanation for the subtropical gyres. However, my colleague's remarks provide us with an opportunity to highlight why we should focus on fluid dynamics, equations, and idealized modeling.
Solid plate reasoning hides complex dynamics. When the wind blows over the ocean, the first effect is not to make it spin. Winds first generate horizontal currents limited to the upper 50-100 m of the ocean. Somewhat unintuitively, these currents, called Ekman currents, run at right angles to and to the right of the wind (in the Northern Hemisphere). The Ekman Currents meet around 25 degrees north latitude, creating a bulge on the ocean surface between the jet stream and the trade winds, as well as a downward motion. we (Water cannot accumulate on the surface forever). This is where we use the Sverdrup scale version:
βV = fwe
where f is the Coriolis parameter (Secondals is spinning in itself), V It's the north–Nanliu Abyss ocean and beta Represents the variation of the Coriolis parameter with latitude.
Fundamentally, the parameter β represents a geometric effect: the earth is a sphere. If the Earth were flat, β would be zero. A particularly important direction for dynamics is the direction along the axis of rotation. The spherical shape of the Earth means that, even in flat-bottomed oceans, the water column aligned with the axis of rotation is smaller near the poles than near the equator (Fig. 2a).

Figure 2: Schematic diagram of the height change of the water column in the direction of the rotation axis. Case a) corresponds to a flat-bottomed ocean where the ocean depth is the same everywhere in the direction of gravity. Scenarios b) and c) illustrate what happens when the seafloor tilts in certain areas of the Earth.
We can now explain Sverdrup equilibrium (1). Wind pushes water down into the interior of the ocean (we <0) makes the water column higher. As a result, the water column must move southward to accommodate the new height. In fact, we see in the real ocean (Fig. 1) that the southward movement of the ocean occurs over the entire width of the basin and only in a very narrow area on the western side of the basin (in the Kuroshio Current, the Gulf Stream, the Agalloch Current Sri Lankan currents, etc.).
Obviously, we can't conduct experiments with real oceans to test our understanding. However, we can do this in numerical models that solve equations that are more complex than Eq. (1) (Nonetheless, we can make some simplifications to make things easier).
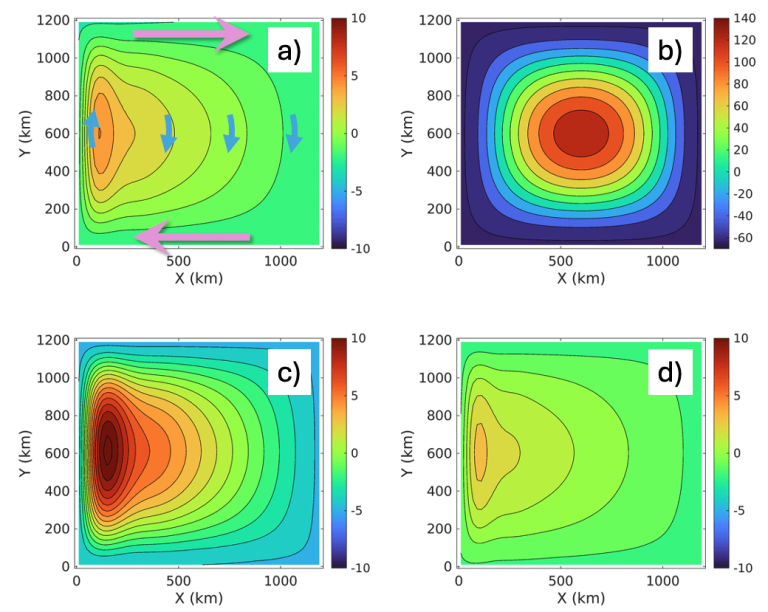
This is illustrated in Figure 3 using a flat-bottomed square basin. Assume that the ocean has uniform density. It is driven by easterly winds in the north of the basin and westerly winds in the south, mimicking real-world wind patterns. Figure 3a shows that, except for a very narrow current at the western boundary, the circulation throughout the basin is southward.

Figure 3: Simulation using a numerical ocean model (MITgcm, mitgcm.org). The pink arrow in the upper left panel shows wind direction. The blue arrow indicates the direction of current flow. The upper row has a flat-bottomed ocean with (a) and without (b) the beta effect. The bottom row, the seafloor is tilted, the northern part of the basin is shallower (corresponding to Figure 2c)), and the southern part of the basin is shallower (corresponding to Figure 2b)
What happens if we set β to zero, meaning that the Earth is flat? As shown in Figure 3b (same wind as in Figure 3a): the circulation becomes a circle around the center of the basin. The water flows south on one half of the basin and north on the other half, completely unlike a real ocean.
A geometric interpretation of β suggests that the shape of the seafloor may play a role here. Imagine that in some areas of the ocean, the ocean floor gets deeper and deeper as you move north. Therefore, from the perspective of the sphere, the water column in this region has a similar height (Fig. 2b). The tilted underlying layer makes the Earth “flatter” in the region. This effect is called the topographic beta effect. In this case it will partially cancel out the effect. For a given wind, the columns need to move south faster than before to accommodate the accumulation of water brought by the wind. Therefore, the circulation must be stronger.
On the contrary, if the seafloor in some areas becomes shallower towards the north (Figure 2c), the height of the water column changes more, and the Earth becomes more “spherical”. The beta effect of topography enhances the normal beta effect, and we predict that the circulation should be weaker than in flat-bottomed oceans.
Likewise, we can test our predictions through numerical experiments. Figures 3c) and d) show the loop in our simplified geometry, but now with a sloped bottom. As predicted, the gyration in Figure 3c (corresponding to the tilt in Figure 2b) is stronger than the flat bottom, while the gyration in Figure 3d (corresponding to the tilt in Figure 2c) is weaker than the flat bottom.
Therefore, the beta effect is crucial in explaining the characteristic patterns of subtropical circulation. There's something we can't get from “correlation” analysis. One can do much more with this theory. More analytical advances can be made, showing that β also controls the width of the narrow western boundary flow (the smaller β, the wider the boundary flow). By the way, analytical solutions can be used to test numerical models (and happily the discretizations used in climate predictions are credible). In retrospect, the correlation analysis of wind patterns and circulation does not seem to tell us much of interest.
The vortex dynamics discussed above was completed decades ago and is now almost textbook material, but the theory still needs to be developed for new research. Recently, we explored the link between Arctic sea ice loss and ocean heat transport under climate change (Aylmer et al., 2024). Climate models predicting large future sea ice reductions will also result in large increases in ocean heat transport into the Arctic. This sounds intuitively correct, but is it really the case? Is this quantitatively possible? That is, is the extra heat in the Arctic Ocean enough to explain the extra melting in these models? Less intuitively, models that predict the atmosphere transporting more heat to the Arctic tend to show relatively little sea ice retreat. These correlations have been of interest for decades, but their explanation remains speculative. Aylmer et al. (2024) provide a theoretical framework that can quantitatively predict the behavior of climate models, providing a solid basis for interpretation.
Interestingly, this work began in 2019, when Dr. Jake Aylmer developed the climate analysis model (published in Aylmer et al., 2020) during the first year of his PhD.
Yes, it takes time. As our field increasingly shifts towards statistical analysis, big data, and funding agencies driving more applied, impactful research (with knock-on effects on PhD training programmes), there is less and less room for this type of work .
As I am putting this blog together, I am listening to a seminar given by David Karoly discussing Hoskins and Karoly (1981), a paper that has had a huge impact on the fields of meteorology and climate dynamics. This paper has been cited over 3000 times and is still cited 100 times a year 40 years after publication! David Karoly points out that this work has significant limitations and should be rigorously evaluated before citation. Hoskins and Karoly (1981) are based on mathematics, geophysical fluid dynamics, and idealized experiments. People need to be trained in these areas to critically evaluate and conduct basic research in climate science. Unfortunately, the number of doctoral students trained in these skills is dwindling.
Correlation analysis is cool, but some of the theory above is even cooler.
refer to:
Aylmer, J., D. Ferreira, and D. Feltham, 2020: Impact of oceanic and atmospheric heat transport on sea ice extent. J.Climate, 33. 7197–7215. https://doi.org/10.1175/JCLI-D-19-0761.1
Aylmer, J., D. Ferreira, and D. Feltham, 2024: Ocean heat transport modulates Arctic sea ice loss. in the news nature communications. https://doi.org/10.21203/rs.3.rs-3249087/v1
Hoskins, BJ and DJ Karoly, 1981: Stable linear response of a spherical atmosphere to thermal and orographic forcing. J. Atmos. science, 38. 1179–1196, https://doi.org/10.1175/1520-0469(1981)038<1179:TSLROA>2.0.CO;2.
Maximenko, N., P. Niiler, M.-H. Rio, O. Melnichenko, L. Centurioni, D. Chambers, V. Zlotnicki and B. Galperin, 2009: Ocean mean dynamic topography from satellite and drifting buoy data using three different techniques. J. Atmos. marine technology, 26(9), 1910-1919. Digital number: https://doi.org/10.1175/2009JTECHO672.1
This article was published in Climate Categories. Bookmark the permanent link.