go through: professor. Remy Taylor
It is known that atmospheric winds and ocean currents ultimately capture energy from the sun. Generally speaking, this involves a two-step process in which solar energy is first converted into potential energy (PE) and then into kinetic energy (KE). However, some aspects of this transition remain mysterious and poorly understood, related to the so-called “cooling paradox.” In the ocean, cooling at high latitudes creates dense water that sinks and creates the Atlantic Meridional Overturning Circulation (AMOC). The difficulty here is that cooling reduces the PE of the ocean. So how to convert it to KE?
The cooling paradox has been a recurring source of confusion and controversy in energetic studies of the atmosphere and ocean, so much so that one of the most famous textbooks on buoyancy-driven flows (Turner, 1973) distanced itself entirely from energetics. It was not until the work of Lorenz (1955) that the cooling paradox began to be resolved. Lorentz's main contribution was to point out that certain configurations (such as the equilibrium rest state shown in the right panel of Figure 1) possess large amounts of potential energy, but none of them can be easily converted into KE.

Figure 1. Schematic representation of the potential temperature field in the atmosphere. The image on the left shows that in actual conditions, potential temperature varies with latitude, with cold air at the polar surface (indicated in purple). The image on the right shows the reference or global equilibrium state of the atmosphere, obtained by letting each layer relax to its equilibrium state while maintaining its mass and potential temperature. The equilibrium state is horizontally uniform and therefore a function of height or pressure only. Reprinted from Tailleux (2013).
Another way to look at the problem is to consider the two fluid configurations shown in Figure 2. Therefore Lorentz postulated that potential energy must be divided into two different forms: available potential energy (APE) and background potential energy (BPE):
PE = APE + BPE
Figure 2. Schematic showing two idealized layerings with the same potential energy (PE) but different partitions APE/BPE. Intuitively, the fluid on the left is purely static and has no APE. No motion is expected. However, the fluid on the right is clearly unstable, and intuitively one would expect the fluid in the upper right corner to start sinking due to being denser than the other plots. The liquid on the right has an APE, while the liquid on the left does not, even though both liquids have the same PE. Reprinted from Hughes et al. (2009).
Lorenz's APE theory solves the cooling paradox because although cooling at high latitudes will reduce the PE and BPE of the ocean, it will increase the APE, which is most important because this is the part of the PE that can be converted into KE .
Although Lorenz's discovery was revolutionary and greatly changed the study of energetics in the ocean and atmosphere, this is not to say that everyone is satisfied with the formulation of Lorenz's APE theory. In fact, whereas kinetic energy can be defined for a single fluid block, Lorenz APE can only be defined for the entire fluid. This is a significant issue that prompts a search for local principles. Understanding how to do this took more than two decades, as the first satisfactory theory of localized APE did not appear until 1981, as reviewed by Tailleux (2013). However, these early formulations remained relatively obscure and complex. It took more than two decades for local APE theory to be digested and reformulated before it began to be applied in practical applications. A key process that can only be discussed using local APE theory is the advection or transport of APE between different regions. Two PhD students in meteorology recently argued that APE advection is critical to understanding the energetics of atmospheric storm tracks (Novak and Tailleux, 2008) and tropical cyclone intensification (Harris et al., 2022). The usefulness and importance of frameworks.
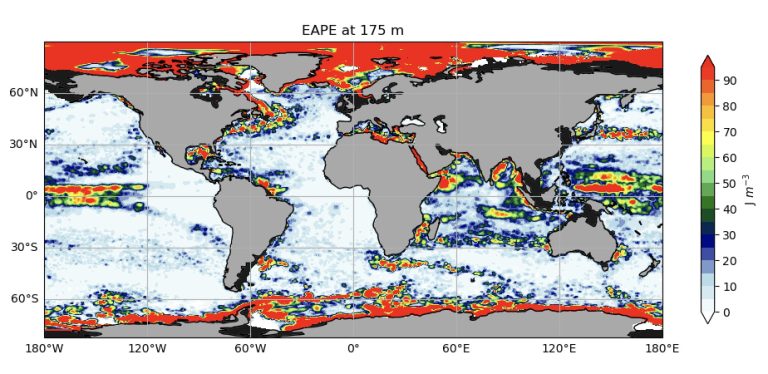
Another advantage of the locally defined APE is that it can be divided into “average” and “eddy” components, similar to what is usually done with kinetic energy. In the atmosphere, the average APE and kinetic energy (KE), as shown in Figure 3, can characterize the large-scale circulation of the atmosphere, while the eddy component characterizes the storm path, that is, the area dominated by low-pressure systems. In the ocean, one can similarly diagnose eddy APEs, which also characterize the ocean's storm tracks, as shown in Figure 4 .

Figure 3. Average and eddy components of available potential and kinetic energy in the Northern Hemisphere. (a) Average APE, (b) average KE, (c) eddy APE, (d) eddy KE. Figure 5.8 reproduced from Novak (2016).
To date, the power and utility of the native APE framework have been used in only a few studies and therefore remain underutilized. Local theories of APE are not yet fully established and are still evolving (Tailleux, 2018). Nonetheless, it is now clear that it represents a better framework than Lorenz's global APE theory, but more work needs to be done to unlock its full potential.

Figure 4. Eddy APE at 175 m estimated from monthly Armor3D data. Areas of strong mesoscale eddy activity are shown in red. Areas of note are the Gulf Stream and Kuroshio areas and the Southern Ocean.
References and further reading:
Harris, BL, R. Tailleux, C.E. Holloway, and P.L. Vidale, 2022. J. Atm. Science, 79, 2493—2513
Hughes, G., O, AM Hogg, and RW Griffiths, 2009: Available potential energy and irreversible mixing in meridional overturning circulation. J. Phys. Oceanography, 39, 31300–3146.
Lorenz, E. N., 1955. Telles, 7, 157–167.
Novak, L., 2016. PhD thesis. University of Reading.
Novak, L and R. Tailleux, 2008: A local view of atmospheric potential energy. J. Atm. Science, 75, 1891–1907.
Tailleux, R., 2013. Annual Review of Fluid Mechanics. 45, 35-58.
Tailleux, R., 2018. Journal of Fluid Mechanics, 842, R1.
Turner, J.S., 1973. Cambridge University Press.